传送门

题意

给你一个图，问其是否有一个子图使得每个点的度恰好为指定的度。

思路

此题有两种解法，一种是正统的带花树解法，还有一种是网络流。

1

带花树用于一般图的最大匹配，比起二分图，一般图多出了环，所以我们只需要考虑环的处理，如果是偶环不会影响正常求解，只需要考虑奇环的情况，为什么呢。
我们在寻找增广路的时候，会将路径上的点黑白染色，匹配只存在黑点与白点之间。
如果没有环或者只有偶环，那么每个点的颜色（或者说奇偶性）是确定的
但如果出现了奇环，那么点的颜色就不再确定，因为奇环顺时针走一圈和逆时针走一圈的结果是不同的。
带花树算法仍然是从每个未匹配的点开始寻找增广路，不过我们采用BFS的方式，每个点均设为无色，端点染成黑色
设当前点为u（黑色）,枚举与它相邻的点v
考虑v是否已经被访问过：
若v尚未访问过（v为无色）
如果v尚未匹配，说明我们找到了一条增广路，直接返回修改。
如果v已经匹配，那么将v染成白色，v的匹配点x加入队列，继续寻找增广路，x染成黑色。
容易看出，根据上面的过程，我们只会对于黑点枚举出边，正确性是显然的，并且我们访问的路径形成了一棵黑白点交错的树。
若v已经访问过（有颜色），说明我们找到了一个环。
如果它是一个偶环（v为白色），那么v显然已经被找过了，无需再找一次。
如果它是一个奇环（v为黑色），就需要采用带花树的特殊处理了。

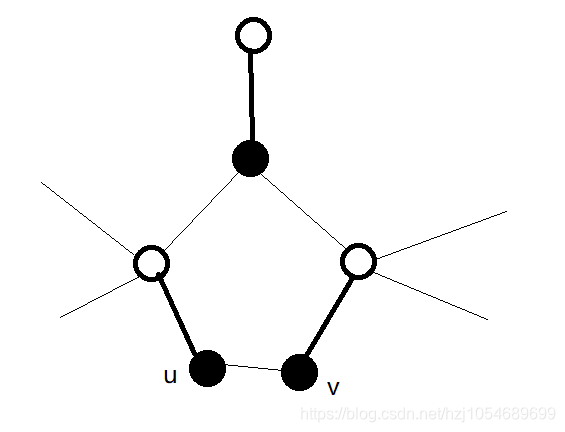
如上图，粗边为匹配边。
对于一个奇环，我们一定是从一个黑点进入，然后也在黑点碰头(u,v)，（这个可以画图理解一下，如果不是从黑点进入，我们在之前访问这个奇环时一定还没有绕一圈就找到增广路增广了）
问题在于，此时对于整个奇环的颜色都不确定了，我们令这个奇环的顶点为最顶上的那一个黑点，那么考虑u上方的这一个白点，我们既可以走从顶点走一条非匹配边到它，它作为一个黑点，也可以从另一边转一圈到它，此时这个它变成了黑点，它是需要加入队列继续走的
也就是说，对于一个奇环，它上面的点都可以成为黑点。
继续观察可以发现，整个奇环的匹配状态只与顶点的匹配状态有关，如果在后来的某一次寻找时奇环上的匹配被改变了，那么顶点的颜色唯一决定了整个环的匹配边是如何走的。
也就是说，整个环就可以用一个顶点表示了，也就意味着我们可以将这个环缩掉，缩掉的环就称为“花”，缩环就是开花
我们不妨对于每一个白点x，记pre[x]表示x是由哪一个黑点走过来的，也就是记录了增广路上的非匹配边。
对于每一个点，记match[x]表示x的匹配点是谁。
缩环具体怎么缩呢？
如果直接修改原本的连边比较麻烦，我们考虑采用并查集，记录每个点所在的奇环的顶点，初始时就是它自己。缩环的时候，我们直接将环上的所有点并查集父亲连向奇环的顶点，并将环上的白点都变成黑点，并且加入队列。
此外，由于奇环可以双向走，因此我们的pre边也要变成双向的。
容易发现，我们有可能经过了多次缩环，也就是说某一次缩环的一个点很有可能是缩过的一个环顶，我们在缩环以及找到增广路返回修改的时候是需要走原来缩之前的环的，这个只需要沿着pre和match一直走即可，pre在这里相当于记录了缩掉的环内部的走法。
现在我们来理一理思路
从每个未匹配的点BFS寻找增广路，每个点均设为无色，端点染成黑色
枚举与当前点u（黑色）相邻的点v
考虑v是否已经被访问过
若v尚未访问过（v为无色）
如果v尚未匹配，找到了一条增广路，直接返回修改。
如果v已经匹配，将v染成白色，将v的匹配点x加入队列，继续寻找增广路，x染成黑色。
若v在当次增广已经访问过，找到环
v为白色，是一个偶环，跳过。
v为黑色且u,v所在的奇环已经缩过了，那么也跳过。
否则，v为黑色，找到一个新的奇环，那么找到u,v所在奇环的环顶（即它们在BFS上跑出来的交错树的lca，称之为最近公共花祖先），将u到环顶的路径以及v到环顶的路径修改掉，白点染成黑点，加入队列，并将环上的点（或者是某个已经缩了的环顶）并查集父亲指向lca。
上面就是带花树的一些解释了，这里参考了很多博客才理解的，上面内容也是取自这些博客。

关于这个题其实也有原题hdu3551,比较有技巧的地方就是建图，把每个点都拆分成题目所要求的度数个点（我们暂且称这些点为分点），把每条边也拆成两个点，例如边（u，v）拆成点两个点a，b，a与u的所有分点相连，b与v的所有分点相连。a，b也连一条边。建好图后求一个完美匹配即可，为什么是完美匹配呢，因为对于每一个点u，如果其分点都能匹配到，则匹配的相应边的另一点也能与另一点的分点匹配，而没有与分点匹配的边的两个点会自己与自己匹配。这样找到的一个完美匹配就是答案。

#include<bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
const int N = 110, M = 410;
vector<int> e[N];
int n, m;
int d[N];
int idx;
PII edge[N];
vector<int> du[N];

bool Graph[M][M];
int Match[M];
bool InQueue[M], InPath[M], InBlossom[M];
int Head, Tail;
int Queue[M];
int Start, Finish;
int NewBase;
int Father[M], Base[M];
int Count;

void init() {
    for(int i = 1; i <= n; i++) {
        e[i].clear();
        du[i].clear();
    }
    memset(d, 0, sizeof d);
    memset(edge, 0, sizeof edge);
    memset(Graph, 0, sizeof Graph);
    memset(Match, 0, sizeof Match);
    memset(InQueue, 0, sizeof InQueue);
    memset(InPath, 0, sizeof InPath);
    memset(InBlossom, 0, sizeof InBlossom);
    memset(Queue, 0, sizeof Queue);
    memset(Father, 0, sizeof Father);
    memset(Base, 0, sizeof Base);
    Count = Start = Finish = NewBase = Head = Tail = idx = 0;
}

void CreatGraph() {//建图
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= d[i]; j++) {
            du[i].push_back(++idx);
        }
    }
    for(int i = 1; i <= m; i++) {
        int u = edge[i].first, v = edge[i].second;
        int a = ++idx, b = ++idx;
        Graph[a][b] = Graph[b][a] = 1;
        for(int j = 0; j < du[u].size(); j++) {
            int x = du[u][j];
            Graph[a][x] = Graph[x][a] = 1;
        }
        for(int j = 0; j < du[v].size(); j++) {
            int x = du[v][j];
            Graph[b][x] = Graph[x][b] = 1;
        }
    }
}


void Push(int u) {
    Queue[Tail] = u;
    Tail++;
    InQueue[u] = true;
}

int Pop() {
    int res = Queue[Head];
    Head++;
    return res;
}
//下面都是带花树模板
int FindCommonAncestor(int u, int v) {//寻找最近公共花祖先lca
    memset(InPath, false, sizeof(InPath));
    while(true) {
        u = Base[u];
        InPath[u] = true;
        if(u == Start) break;
        u = Father[Match[u]];
    }
    while(true) {
        v = Base[v];
        if(InPath[v]) break;
        v = Father[Match[v]];
    }
    return v;
}

void ResetTrace(int u) {
    int v;
    while(Base[u] != NewBase) {
        v = Match[u];
        InBlossom[Base[u]] = InBlossom[Base[v]] = true;
        u = Father[v];
        if(Base[u] != NewBase) Father[u] = v;
    }
}

void BloosomContract(int u, int v) {
    NewBase = FindCommonAncestor(u, v);
    memset(InBlossom, false, sizeof(InBlossom));
    ResetTrace(u);
    ResetTrace(v);
    if(Base[u] != NewBase) Father[u] = v;
    if(Base[v] != NewBase) Father[v] = u;
    for(int tu = 1; tu <= idx; tu++) {
        if(InBlossom[Base[tu]]) {
            Base[tu] = NewBase;
            if(!InQueue[tu]) Push(tu);
        }
    }
}

void FindAugmentingPath() {
    memset(InQueue, false, sizeof(InQueue));
    memset(Father, 0, sizeof Father);
    for(int i = 1; i <= idx; i++) Base[i] = i;
    Head = Tail = 1;
    Push(Start);
    Finish = 0;
    while(Head < Tail) {
        int u = Pop();
        for(int v = 1; v <= idx; v++) {

            if(Graph[u][v] && (Base[u] != Base[v]) && (Match[u] != v)) {

                if((v == Start) || ((Match[v] > 0) && Father[Match[v]] > 0)) {
                    BloosomContract(u, v);
                }
                else if(Father[v] == 0) {
                    Father[v] = u;
                    if(Match[v] > 0) Push(Match[v]);
                    else {
                        Finish = v;
                        return;
                    }
                }
            }
        }
    }
}

void AugmentPath() {
    int u, v, w;
    u = Finish;
    while(u > 0) {
        v = Father[u];
        w = Match[v];
        Match[v] = u;
        Match[u] = v;
        u = w;
    }
}

void Edmonds() {
    memset(Match, 0, sizeof Match);
    for(int u = 1; u <= idx; u++) {
        if(Match[u] == 0) {
            Start = u;
            FindAugmentingPath();
            if(Finish > 0) AugmentPath();
        }
    }
}

void PrintMatch() {
    Count = 0;
    for(int u = 1; u <= idx; u++) {
        if(Match[u] > 0) Count++;
    }
    if(Count == idx) puts("Yes");
    else puts("No");
}

void solve() {
    CreatGraph();
    Edmonds();
    PrintMatch();
}

int main() {
    freopen("in.txt", "r", stdin);
    while(~scanf("%d%d", &n, &m)) {
        init();
        for(int i = 1; i <= n; i++) {
            scanf("%d", &d[i]);
        }
        for(int i = 1; i <= m; i++) {
            int u, v;
            scanf("%d%d", &u, &v);
            e[u].push_back(v);
            e[v].push_back(u);
            edge[i] = {u, v};
        }
        solve();
    }
    return 0;
}

2

第二种方法虽然不是正解，也提一下，利用一个超级源点和超级汇点，点与点建边，每个点拆成i和i'，源点和i连一条权值为di的边，i'和汇点连一条权值为di的边，对于m条边，u和v，u于v'建边，v与u'建边，这样每个点的流量都只能流到其他点，最大流就是让每个点都选了di条边。如果流出源点和流入汇点的值相等则判断是合理的。

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
struct EDGE {
	int to, w, next;
} edge[2000];
int cnt;
int head[2000];
int deep[2000];

void init() {
	cnt = 0;
	memset(head, -1, sizeof(head));
}

void addedge(int u, int v, int w) {
	edge[cnt].to=v; edge[cnt].w=w; edge[cnt].next=head[u]; head[u]=cnt++;
	edge[cnt].to=u; edge[cnt].w=0; edge[cnt].next=head[v]; head[v]=cnt++;
}

int bfs(int s, int t) {
	queue<int> q;
	memset(deep, 0, sizeof(deep));
	q.push(s);
	deep[s] = 1;
	int top;
	while(!q.empty()) {
		top = q.front();
		q.pop();
		for(int i = head[top];i+1; i = edge[i].next) {
			int v = edge[i].to;
			int w = edge[i].w;
			if(!deep[v]&&w) {
				deep[v] = deep[top]+1;
				q.push(v);
			}
		}
	}
	return deep[t];
}

int dfs(int s, int t, int inflow) {
	if(s==t) return inflow;
	int acflow=0;
	for(int i=head[s]; i+1; i=edge[i].next) {
		if(edge[i].w && deep[s]+1 == deep[edge[i].to]) {
			int x = dfs(edge[i].to,t,min(inflow, edge[i].w));
			if(x>0) {
				acflow+=x; inflow-=x;edge[i].w -= x; edge[i^1].w += x;
				if(!inflow) break;
			}
		}
	}
	if(!acflow) deep[s] = -2;
	return acflow;
}

int dinic(int s,int t) {
	int f = 0;
	while(bfs(s,t)) f += dfs(s,t,INF);
	return f;
}

int n, m, a, b;
int d[55];

int main() {
	while(~scanf("%d %d", &n, &m)) {
		init();
		int sum = 0;
		for(int i = 1;i <= n; i++) {
			scanf("%d", &d[i]);
			sum += d[i];
			addedge(0, i, d[i]);
		}
		
		int l = 1e9, r = 0;
		for(int i = 1;i <= m; i++) {
			scanf("%d %d", &a, &b);
			addedge(a, b+n, 1);
			l = min(l, b+n); r = max(r, b+n);
			addedge(b, a+n, 1);
			l = min(l, a+n); r = max(r, a+n);
		}
		
		int fin = r+1;
		for(int i = l;i <= r; i++) {
			addedge(i, fin, d[i-n]);
		}
		
		printf("%s\n", dinic(0, fin)==sum?"Yes":"No");
	}
}