传送门

题意

给定n个由B和N组成的字符串s1，s2……sn，一个字符串每次可以做以下操作中的一个
1.删除或增加一个B
2.删除或增加一个N
3.删除或增加一个BN
4.删除或增加一个NB
求一个由N,B组成的字符串t，要求t转换到所有字符串s的操作次数的最大值最小，使得t与s的B,N字符数量相等。

思路

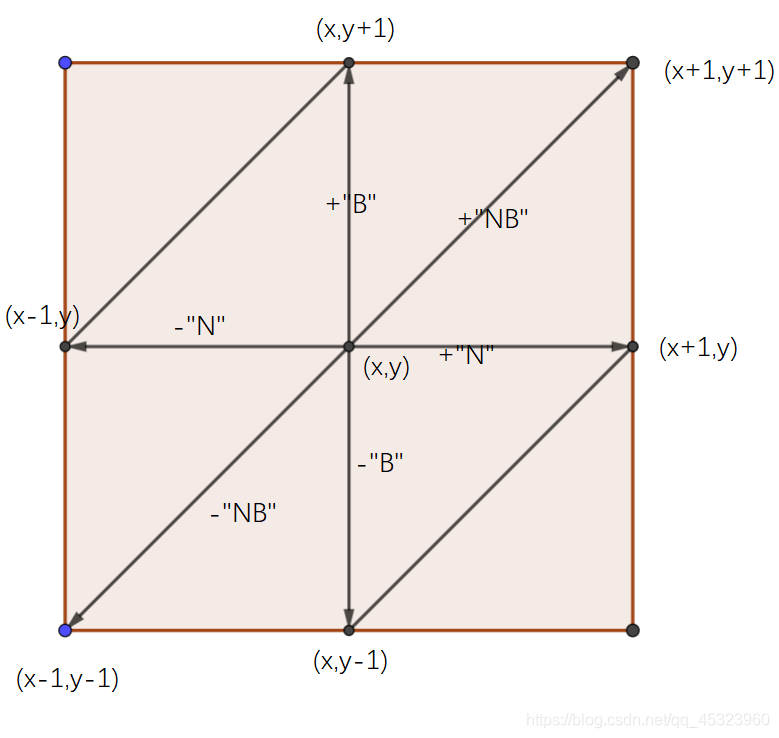
首先一个字符串与其 N、B 的顺序无关，只与 N、B 的数量有关，所以可以表示为平面上一个点 (xi,yi)
求最大值最小考虑二分，这个也很平凡。然后两个点的距离的定义也很显然：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cmath>
#include <vector>
#include <map>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
#define maxn 500005
#define mod 998244353
ll maxa=0,mina=inf,maxb=0,minb=inf,mxd=-inf,mnd=inf;
ll ansb=0,ansn=0;
char s[maxn];

bool check(ll mid){
    ll minx=max(0ll,maxa-mid),maxx=mina+mid,miny=max(0ll,maxb-mid),maxy=minb+mid,maxd=mnd+mid,mind=mxd-mid;
    if(minx>maxx||miny>maxy||mind>maxd) return false;
    if(miny-maxx>maxd||maxy-minx<mind) return false;
    if((maxd>=maxy-maxx)&&(mind<=maxy-maxx)) ansn=maxx,ansb=maxy;
    else if(mind>=maxy-maxx) ansb=maxy,ansn=maxy-mind;
    else{
        ansn=maxx,ansb=maxx+maxd;
    }
    /*if (maxd >= maxy - minx && mind <= miny - maxx) ansn=maxx, ansb=maxy;
    else if (maxd <= maxy - maxx) ansn=maxx, ansb=maxx + maxd;
    else if (maxd <= maxy - minx) ansn=maxy - maxd, ansb=maxy;
    else if (mind >= maxy - maxx) ansn=maxy - mind, ansb=maxy;
    else if (mind >= miny - maxx) ansn=maxx, ansb=maxx + mind;*/
    return true;
}

int main(){
    ll i, n, j, k, t;
    scanf("%lld",&n);
    for(i=1;i<=n;i++){
        scanf("%s",s);
        k=strlen(s);
        ll a=0,b=0;
        for(j=0;j<k;j++){
            if(s[j]=='N') a++;
            else b++;
        }
        mina=min(mina,a),maxa=max(a,maxa);
        minb=min(minb,b),maxb=max(b,maxb);
        mxd=max(mxd,b-a),mnd=min(mnd,b-a);
    }
    ll l=0,r=500005;
    while(l<r){
        ll mid=(l+r)>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    check(l);
    printf("%lld\n",l);
    for(i=1;i<=ansb;i++) printf("B");
    for(i=1;i<=ansn;i++) printf("N");
    printf("\n");
}